14. Hough Transform
title
Using the Hough Transform to Find Lines from Canny Edges
Hough Intro
INSTRUCTOR NOTE:
In image space, a line is plotted as x vs. y, but in 1962, Paul Hough devised a method for representing lines in parameter space, which we will call “Hough space” in his honor.
In Hough space, I can represent my "x vs. y" line as a point in "m vs. b" instead. The Hough Transform is just the conversion from image space to Hough space. So, the characterization of a line in image space will be a single point at the position (m, b) in Hough space.
stuff
So now I’d like to check your intuition… if a line in image space corresponds to a point in Hough space, what would two parallel lines in image space correspond to in Hough space?
nd013 image parallel lines to hough
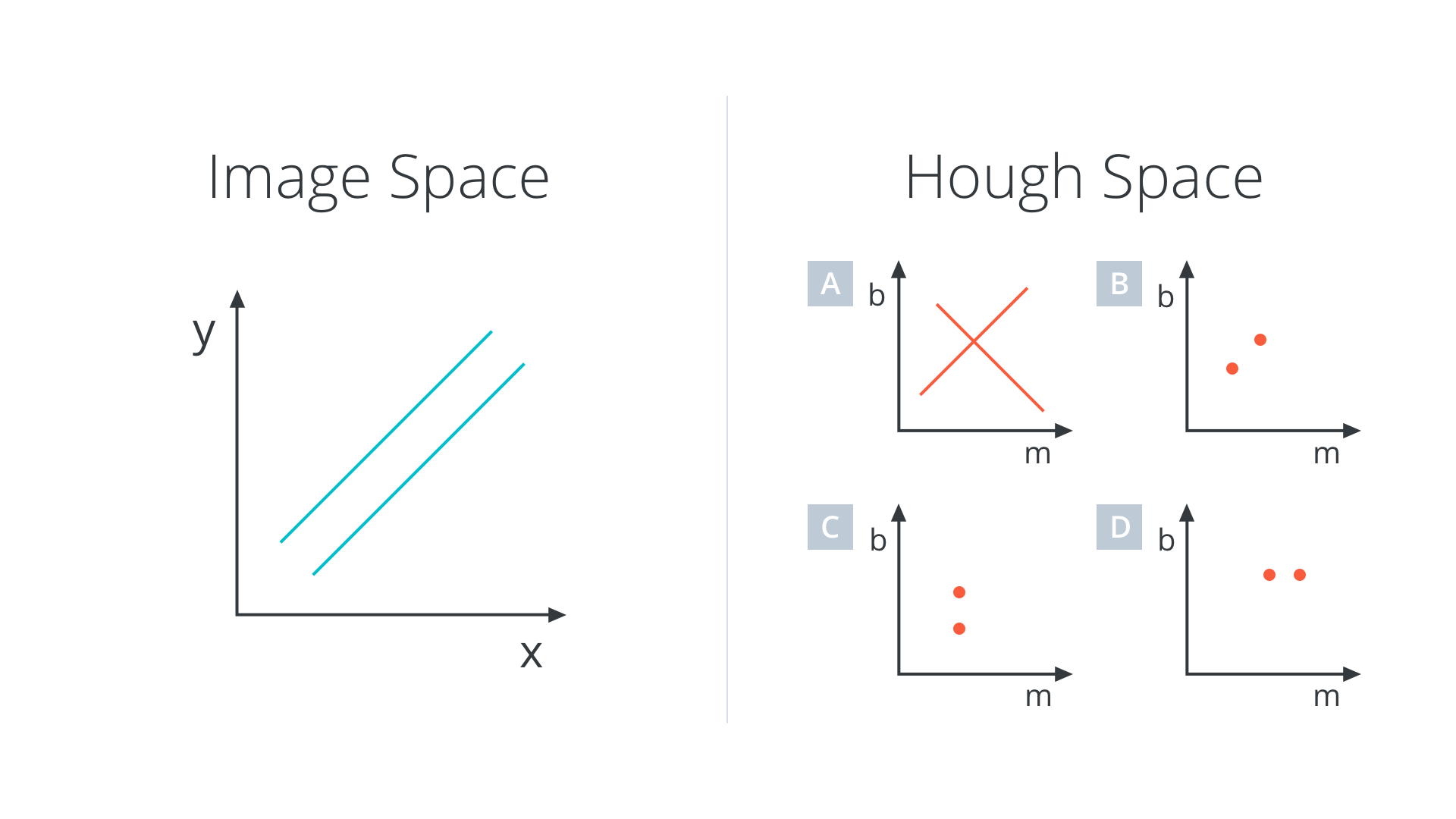
hough_quiz1
SOLUTION:
Chough_text2
Alright, so a line in image space corresponds to a point in Hough space. What does a point in image space correspond to in Hough space?
A single point in image space has many possible lines that pass through it, but not just any lines, only those with particular combinations of the m and b parameters. Rearranging the equation of a line, we find that a single point (x,y) corresponds to the line b = y - xm.
So what is the representation of a point in image space in Hough space?
nd013 image point to hough

hough_quiz2
SOLUTION:
Ahough_text3
What if you have 2 points in image space. What would that look like in Hough space?
nd013 image 2 points

hough_quiz3
SOLUTION:
Chough_text4
Alright, now we have two intersecting lines in Hough Space. How would you represent their intersection at the point (m 0 , b 0 ) in image space?

hough_quiz4
SOLUTION:
A) A line in image space that passes through both (x1, y1) and (x2, y2)sine Hough
title
So, what happens if we run a Hough Transform on an image of a square? What will the corresponding plot in Hough space look like?
Hough Quiz 5
hough_quiz5